Central Limit Theorem

Theorem

Let

• $X_1\dots X_n$ : Observations of a random sample, with
  • Common mean $\mu$
  • Common variance ${\sigma }^2\in \mathbb{P}$

If

Y_{n} & = \frac{ \sum_{i=1}^n X_{i} - n\mu }{\sqrt{ n }\sigma} \\ & = \frac{\bar{X}_{n}-\mu}{\sigma/\sqrt{ n }} \end{align} $$ Then $$ Y_{n}\xrightarrow D N(0,1) $$

Note

Recall that the notation $Y_n\stackrel{D}{\to }N(0,1)$ was introduced in convergence in distribution’s remark.

We often state the central limit theorem as:

$$\sqrt{n}(\bar{X}-\mu )\to N(0,{\sigma }^2)$$

One of the key applications of this theorem is for statistical inference, as shown in Example 5.3.1-5.3.6 in the source book.

Proof

This is $e$

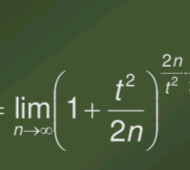
Example

Let $\bar{X}$ denote the mean of a random sample of size $128$ from a Gamma distribution with $\alpha =2$ and $\beta =4$.

Approximate $P(7<\bar{X}<9)$

• $\mu =\alpha \beta =2\cdot 4=8$
• ${\sigma }^2=\alpha {\beta }^2=2\cdot 16=32$
• $\sigma /\sqrt{n}=\sqrt{\frac{32}{128}}=\frac{1}{2}$

By central limit theorem,

$$\begin{array}{rl}P(7<\bar{X}<9)& =P\left(\frac{7-\mu }{\sigma /\sqrt{n}}<\frac{\bar{X}-\mu }{\sigma /\sqrt{n}}<\frac{9-\mu }{\sigma /\sqrt{n}}\right)\\ & =P\left(\frac{7-8}{1/2}<Z<\frac{9-2}{1/2}\right)\\ & =P\left(-2<Z<2\right)\\ & =\Phi (2)-\Phi (-2)\\ & =\Phi (2)-[1-\Phi (2)]\\ & =2\cdot \Phi (2)-1\\ & =2\cdot 0.977-1\\ & =0.954\end{array}$$