1.5 Random Variables

<< 1.4 Conditional Probability and Independence | 1.6 Discrete Random Variables >>

Definition 1.5.1: Random variable

Let

• $\mathcal{C}$ : Sample space
• $X$ : Function

If $X$ assigns each element $c\in \mathcal{C}$ one and only one number $X(c)=x$

Then we say $X$ is a random variable

Link to original

Definition 1.5.2: Cumulative distribution function (cdf)

Definition

Let $X$ : Random variable

If

$$\begin{array}{rl}{F}_X(x)& =P_X((-\infty ,x])\\ & =P(\{c\in \mathcal{C}:X(c)\le x\})\\ & =P(X\le x)\\ & ={\int }_{-\infty }^x{f}_X(t)dt\end{array}$$

Then we say $F_X(x)$ is the cumulative distribution function (cdf) of $X$.

Remark

We often shorten

• $P(\{c\in \mathcal{C}:X(c)\le x\})$ to $P(X\le x)$
• “Cumulative distribution function” to “distribution function” or “cdf”

Link to original

Definition: Equal in distribution

Let $X,Y$ : two random variables

If $F_X(x)=F_Y(x),\forall x\in \mathbb{R}$

Then

• We say $X$ and $Y$ are equal in distribution
• We write $X\stackrel{D}{=}Y$

Theorem 1.5.1

Let

• $X$ : Random variable
• $F_X(x)$ : cdf of $X$

Then

• $\forall a,b\in \mathbb{R},a<b⟹F(a)\le F(b),\forall a,b\in \mathbb{R}$ ($F$ is nondecreasing)
• ${\lim }_{n\to -\infty }F(x)=0$ (lower limit of $F$ is 0)
• ${\lim }_{n\to \infty }F(x)=1$ (upper limit of $F$ is 1)
• ${\lim }_{x\downarrow x_0}F(x)=F(x_0)$ (F is right continuous)

Theorem 1.5.2

Let

• $X$ : Random variable
• $F_X$ : cdf of $X$

Then $P[a<X\le b]=F_X(b)-F_X(a),\forall a<b$

Theorem 1.5.3

For any random variable,

$$P[X=x]=F_X(x)-F_X(x-)$$

$\forall x\in \mathbb{R},F_X(x-)={\lim }_{z\uparrow x}{F}_X(z)$

Remark 1.5.1

The subscript $X$ on $P_X$ and $f_X$ identifies the pmf and pdf, respectively, with the random variable.

If the identity of the random variable is clear, we often suppress the subscripts.

Exercise

Example: Random variable representing sum of 2 dice rolls

Let $X$ be a random variable which represents the sum of rolls from 2 dices. So, $X((a,b))=a+b$, where $a$ and $b$ are rolls from 1st and 2nd dice respectively. In this case, $X$ has value space $\{(1,1),(1,2),\dots ,(6,5),(6,6)\}$, and range $\{2,3,\dots ,12\}$.

Example: pmf of discrete random variable

Let $X$ represent sum of rolls of 2 dices. So $X((x,y))=x+y$. $\mathcal{D}$ of $X$ is $\{2,3,\dots ,12\}$. The pmf of $X$ is

Example: pdf of continuous random variable

Choose a real number at random from the interval $(0,1)$. It is reasonable to assign $P_X[(a,b)]=b-a,\text{for }0<a<b<1$.

Let $X$ be the number chosen. $pdf$ of $X$ is

$$f_X(x)=\{\begin{array}{ll}1& 0<x<1\\ 0& \text{elsewhere.}\end{array}$$

Probability that $X<\frac{1}{8}$ or $X>\frac{7}{8}$ is

$$\begin{array}{rl}P[\{X<\frac{1}{8}\}\cup \{X>\frac{7}{8}\}]& =P[X<\frac{1}{8}]+P[X<\frac{7}{8}]\\ & ={\int }_{-\infty }^{\frac{1}{8}}dx+{\int }_{\frac{7}{8}}^{\infty }dx\\ & ={\int }_{-\infty }^{0}dx+{\int }_0^{\frac{1}{8}}dx+{\int }_{\frac{7}{8}}^{1}dx+{\int }_1^{\infty }dx\\ & =0+{\int }_0^{\frac{1}{8}}dx+{\int }_{\frac{7}{8}}^{0}dx+0\\ & =\frac{1}{4}\end{array}$$

1.6.1.

1.6.2.

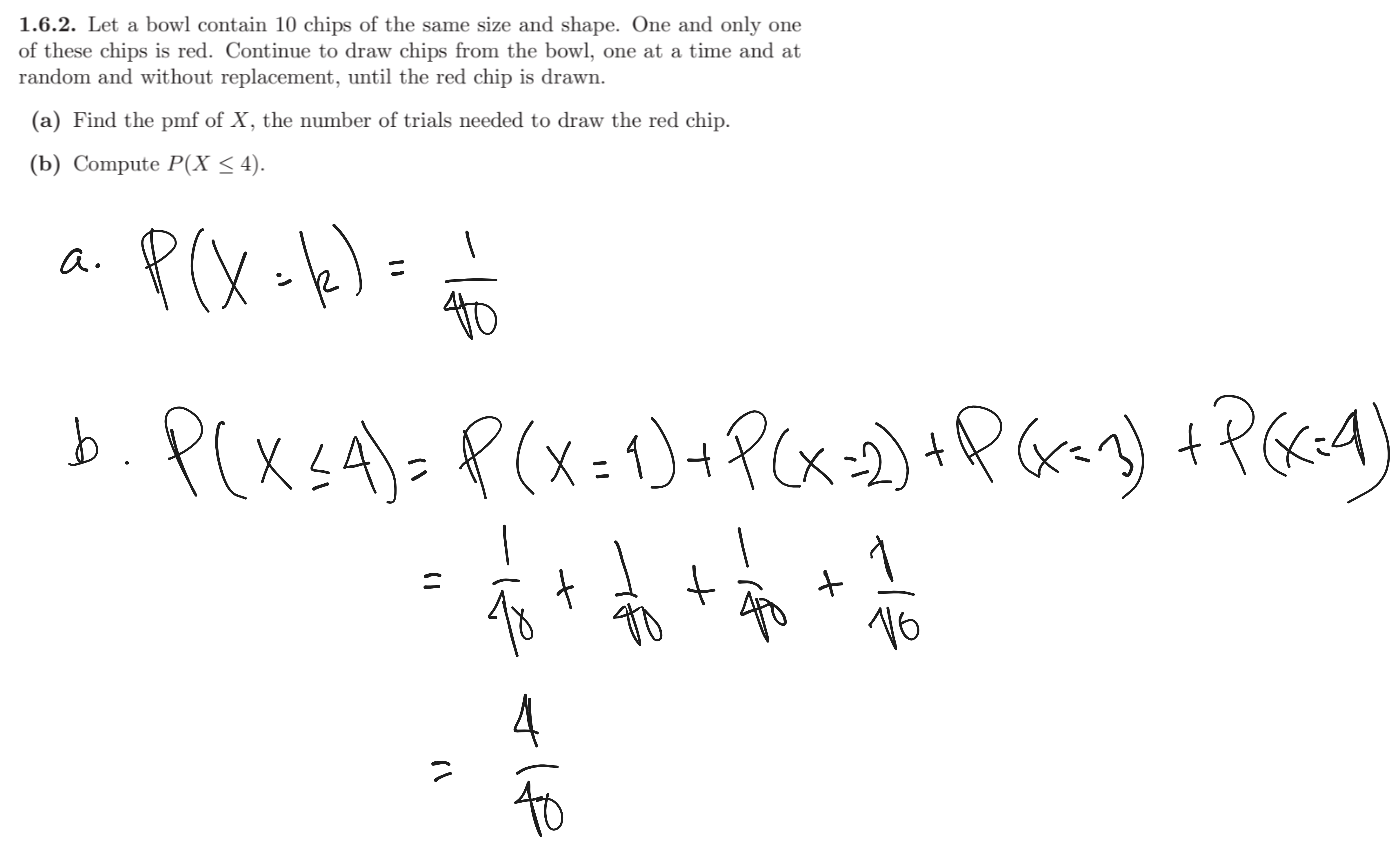
1.6.3.

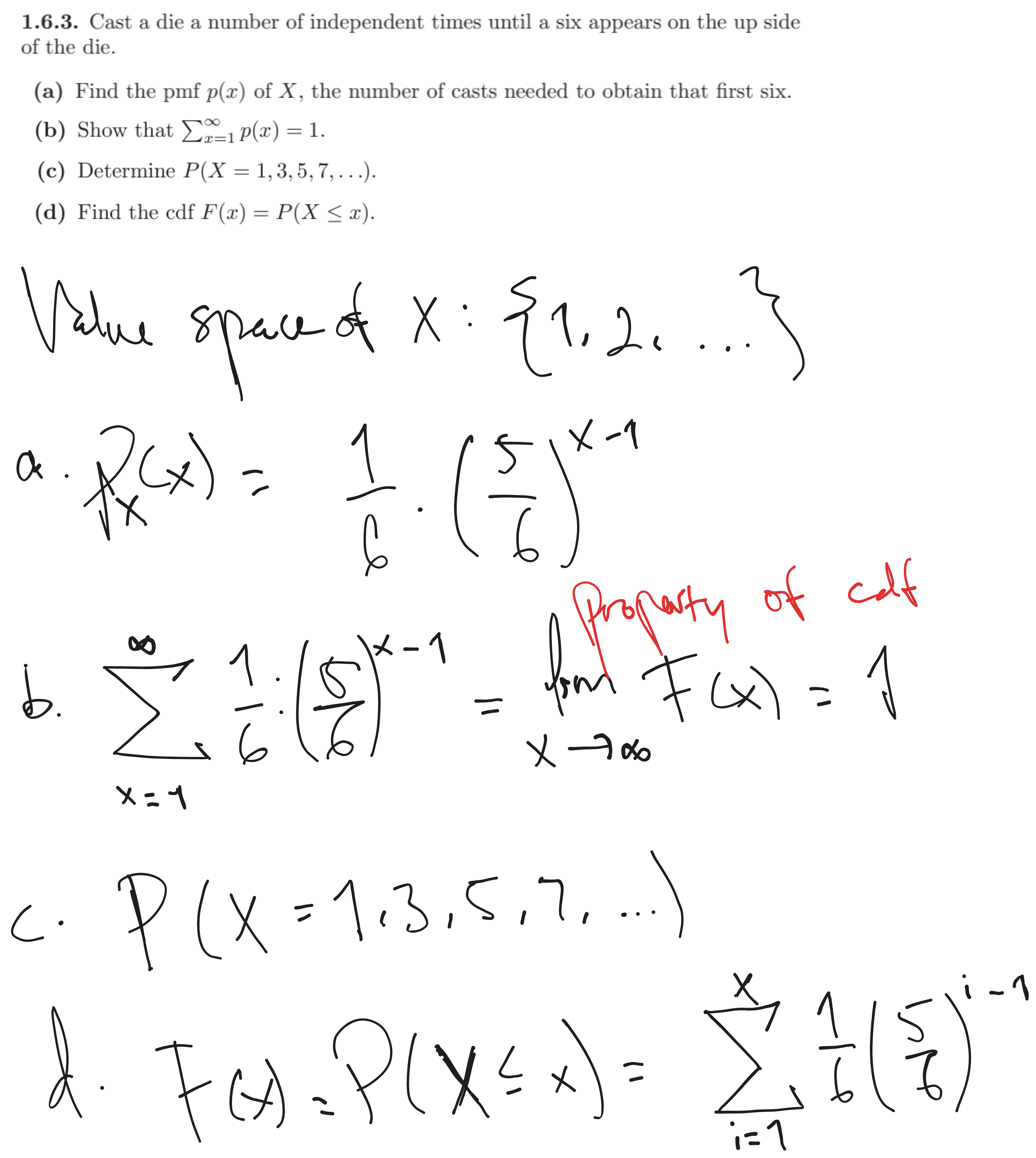
1.6.4.