Assumptions for the Error Component

The $NIID(0,{\sigma }^2)$ (Normally and Independently Identically Distributed) assumption for the error component $({ϵ}_i)$ means:

1. Zero mean ($E(\mathbf{ϵ})=0$)
2. Normal distribution (${ϵ}_i\sim N(0,{\sigma }^2),\forall i\in \{1,\dots ,n\}$)
3. Constant variance ($\mathrm{Var}({ϵ}_i)={\sigma }^2,\forall i\in \{1,\dots ,n\}$)
4. Independency ($\mathrm{Cov}({ϵ}_i,{ϵ}_j)=0,\forall i,j\in \{1,\dots ,n\},i\ne j$)

The above assumptions can be further elaborated as:

1. Zero mean assumption

The error ${ϵ}_i=y_i-({\beta }_0+{\beta }_1{x}_i)$ is the deviation of the estimation to the true value. Thus ideally, the error should be minimized to give the most accurate prediction, i.e., the mean of the error should be as close to 0 as possible.

This is written mathematically as $E({ϵ}_i)=0$. As a result, we may obtain the following expectation for $y_i$:

$$\begin{array}{rlr}E(y_i)& =E({\beta }_0+{\beta }_1{x}_i+{ϵ}_i)& \\ & =E({\beta }_0+{\beta }_1{x}_i)+E({ϵ}_i)& \\ & ={\beta }_0+{\beta }_1{x}_i& \end{array}$$

2. Normally distributed assumption

The model should be as close as possible to each data point. This assumptions prevents overfit or underfit problem.

The error should be small. And if it’s large, the frequency should be less than those with smaller deviation.

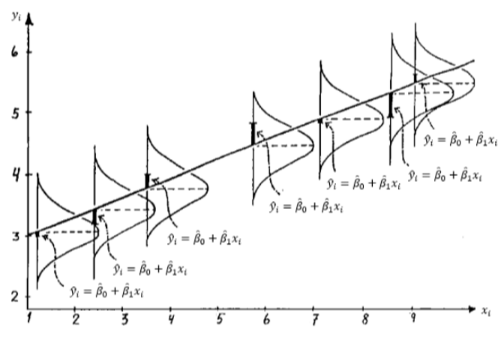
Illustration of normality assumption for error terms

3. Constant variance assumption (homoscedasticity)

Variation of ${ϵ}_i$ (and hence, variation of $y_i$) is the same across conditions represented by $x_i$. In simpler terms, regardless of the value of the predictor $(x_i)$, the spread (variance) of the error term should remain constant.

Example of model that violates the constant variance assumption

4. Independency assumption

An error is not related with others errors; knowing the error for one observation should give no information about the error of another.