Tugas Minggu 5

Nomor 1

1.1

Soal

Estimasi model OLS ($Y$ pada $X_1$, $X_2$). Tentukan koefisien regresi, $SE$, $R^2$.

Secara umum, ordinary least square dari suatu model dapat ditentukan oleh $\hat{\mathbf{\beta }}=({\mathbf{x}}^{\prime }\mathbf{x}{)}^{-1}{\mathbf{x}}^{\prime }\mathbf{y}$. Menggunakan rumus tersebut, diperoleh $\hat{\mathbf{\beta }}$ sebagai berikut:

$$\begin{array}{rl}\hat{\mathbf{\beta }}& ={\left[\begin{array}{ccc}2.2683446& 0.2625189& 0.4693932\end{array}\right]}^{\prime }\end{array}.$$

sehingga diperoleh ${\beta }_0=2.2683446$.

Standard error dapat dicari dengan rumus berikut: $SE(\hat{\mathbf{\beta }})=\sqrt{\text{diag}({\hat{\sigma }}^2({\mathbf{x}}^{\prime }\mathbf{x}{)}^{-1})}$

dimana:

$$\begin{array}{rl}{\hat{\sigma }}^2& =\frac{SSE}{n-k}\\ SSE& =\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2\end{array}$$

Dari rumus tersebut, diperoleh $SE(\hat{\mathbf{\beta }})$ sebagai berikut:

$$\begin{array}{rl}SE({\beta }_0)& =0.13911\\ SE({\beta }_1)& =0.03320\\ SE({\beta }_2)& =0.32665\end{array}$$

Coefficient of Determination ($R^2$) dapat dicari dengan rumus berikut:

$$\begin{array}{rl}{R}^2& =1-\frac{SSE}{SST}\\ & =1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}\end{array}$$

dimana:

$$\begin{array}{rl}SSE& =\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2\\ SST& =\sum _{i=1}^n(y_i-\bar{y}{)}^2\\ {\hat{y}}_i& =X_i\hat{\beta }\end{array}$$

Dari rumus tersebut, diperoleh:

$$R^2=0.99772$$

1.2

Soal

Lakukan uji heteroskedastisitas: Breusch-Pagan dan/atau White test. Jelaskan hasil (statistik & p-value).

Dari uji Breusch-Pagan diperoleh p-value sebagai berikut:

• Lagrange Multiplier p-value: $0.014935$
• F p-value: $0.009695$

Dari uji White diperoleh p-value sebagai berikut:

• Lagrange Multiplier p-value: $0.045105$
• F p-value: $0.024992$

Dari semua hasil tersebut, dapat disimpulkan bahwa terdapat bukti yang cukup untuk mengatakan bahwa error bersifat heteroskedastisitas, sehingga melanggar asumsi homoskedastisitas.

1.3

Soal

Bila heteroskedastisitas ditemukan, berikan dua solusi:

1. SE heteroskedastik-konsisten (robust SE / White),
2. Estimasi GLS.

Diperoleh hasil sebagai berikut:

Variable	OLS Coef	OLS SE	Robust SE	GLS Coef	GLS SE
Intercept	2.268	0.139	0.255	2.180	0.082
$X_1$	0.263	0.033	0.065	0.286	0.026
$X_2$	0.469	0.327	0.649	0.285	0.248
$R^2$	0.9977			0.9985

• Robust SE: Koefisien tidak berubah, tetapi kesalahan standar meningkat signifikan, membuat $X_2$ tidak signifikan secara statistik (nilai-p meningkat).
• GLS: Koefisien dan kesalahan standar berubah. Koefisien $X_2$ turun dari 0.469 ke 0.285, dan GLS memberikan kesalahan standar lebih kecil daripada robust SE.

GLS menghasilkan $R^2$ lebih tinggi (0.9985 vs 0.9977), menunjukkan kecocokan lebih baik.

Gunakan robust standard errors untuk inferensi konservatif tanpa asumsi kuat tentang struktur varians, atau GLS jika efisiensi penting dan model varians spesifik.

1.4

Soal

Plot residual squared vs $X_1$ dan interpretasikan hasilnya.

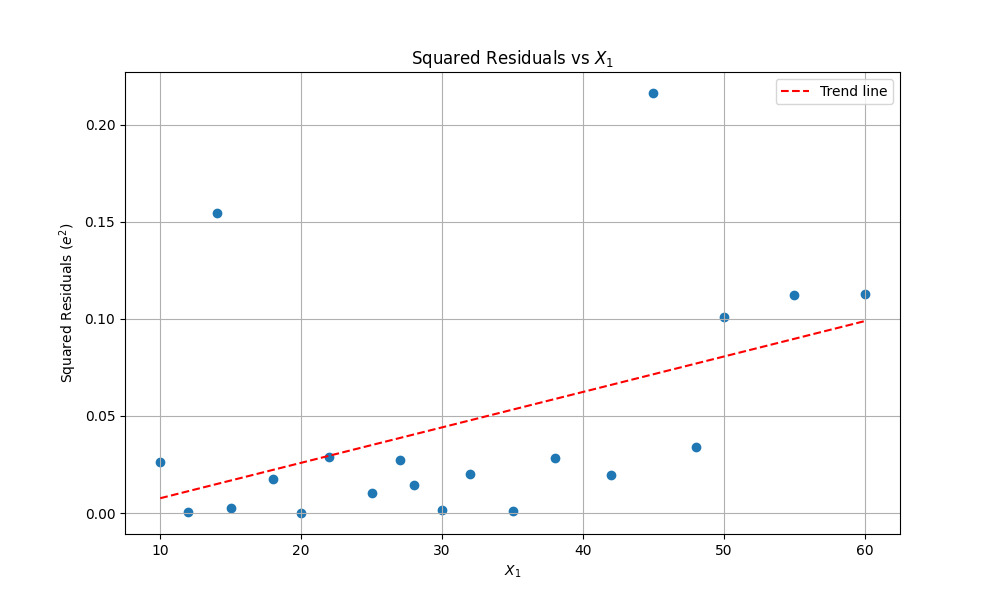
Plot menunjukkan hubungan positif antara pendapatan ($X_1$) dan squared residuals. Garis tren naik mengindikasikan bahwa tingkat pendapatan yang lebih tinggi berhubungan dengan penyimpangan lebih besar dari prediksi model, yang mungkin menunjukkan heteroskedastisitas.

Nomor 2.

2.1

Soal

Estimasi OLS $Y_t=\alpha +\beta X_t+u_t$. Tentukan koefisien regresi dan SE. Estimasi koefisien regresi OLS adalah:

• $\hat{\alpha }=-1.367$
• $\hat{\beta }=0.040$ Kesalahan standar (SE) masing-masing koefisien adalah:
• $SE(\hat{\alpha })=0.402$
• $SE(\hat{\beta })=0.003$

2.2

Soal

Uji autokorelasi: Durbin-Watson dan/atau Breusch-Godfrey (lag 1 atau lag 2). Jelaskan hasil. (Gunakan aturan interpretasi DW).

• Statistik Durbin-Watson: 1.00
• p-value Breusch-Godfrey (lag 1): 0.017
• p-value Breusch-Godfrey (lag 2): 0.042 Statistik DW sebesar 1.00 di bawah nilai kritis bawah (sekitar 1.5 untuk n=30, k=1), menunjukkan adanya autokorelasi positif. p-value dari uji Breusch-Godfrey yang kurang dari 0.05 juga mengkonfirmasi adanya autokorelasi.

2.3

Soal

Jika autokorelasi terdeteksi, terapkan metode GLS untuk model dengan error AR(1) (mis. estimasi $\rho$ dari residual, lalu pakai Cochrane-Orcutt atau Prais-Winsten). Tunjukkan $\hat{\rho }$, koefisien GLS dan bandingkan dengan OLS.

• Estimasi $\hat{\rho }=0.47$
• Koefisien GLS (Cochrane-Orcutt):
  • $\hat{\alpha }=0.562$
  • $\hat{\beta }=-0.004$
• Perbandingan dengan OLS:
  • OLS: $\hat{\alpha }=-1.367$, $\hat{\beta }=0.040$
  • GLS: $\hat{\alpha }=0.562$, $\hat{\beta }=-0.004$ Koefisien GLS berbeda signifikan dari OLS, menunjukkan penyesuaian untuk autokorelasi AR(1).

2.4

Soal

Interpretasikan mengapa autokorelasi mempengaruhi inferensi OLS (efisiensi & SE).

Autokorelasi melanggar asumsi kesalahan independen dalam OLS, menyebabkan estimasi yang tidak efisien dan kesalahan standar yang diremehkan. Hal ini meningkatkan risiko kesalahan Tipe I dalam pengujian hipotesis, sehingga inferensi OLS menjadi tidak dapat diandalkan.