Graph Depth First Search (DFS)

• TODO:
  • Fill “Recursion” algorithm

---

1. Pick some rule for traversing a node.
2. Keep doing it until you reach a dead-end or a node that has already been visited.
3. Backtrack, and visit to a node that is unvisited.
4. Go back to step 2.

Visualization

DFS in tree

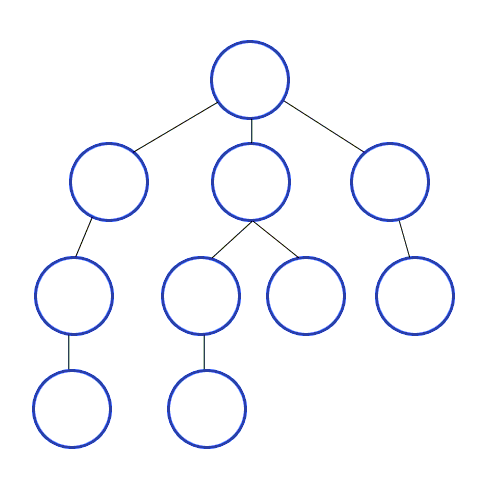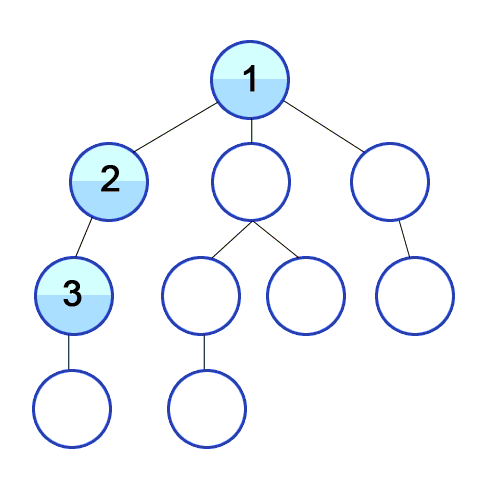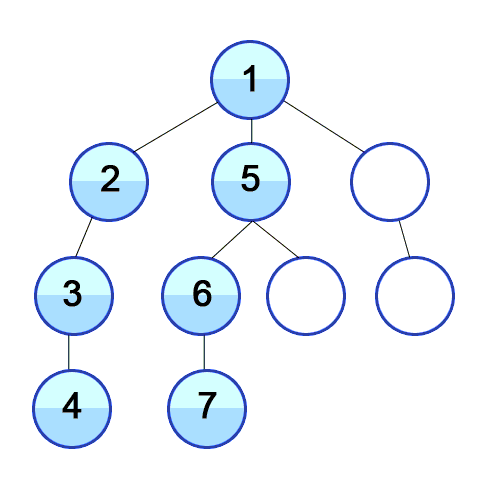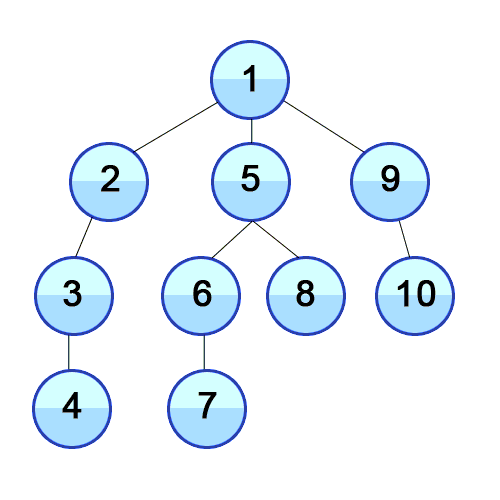
DFS in maze

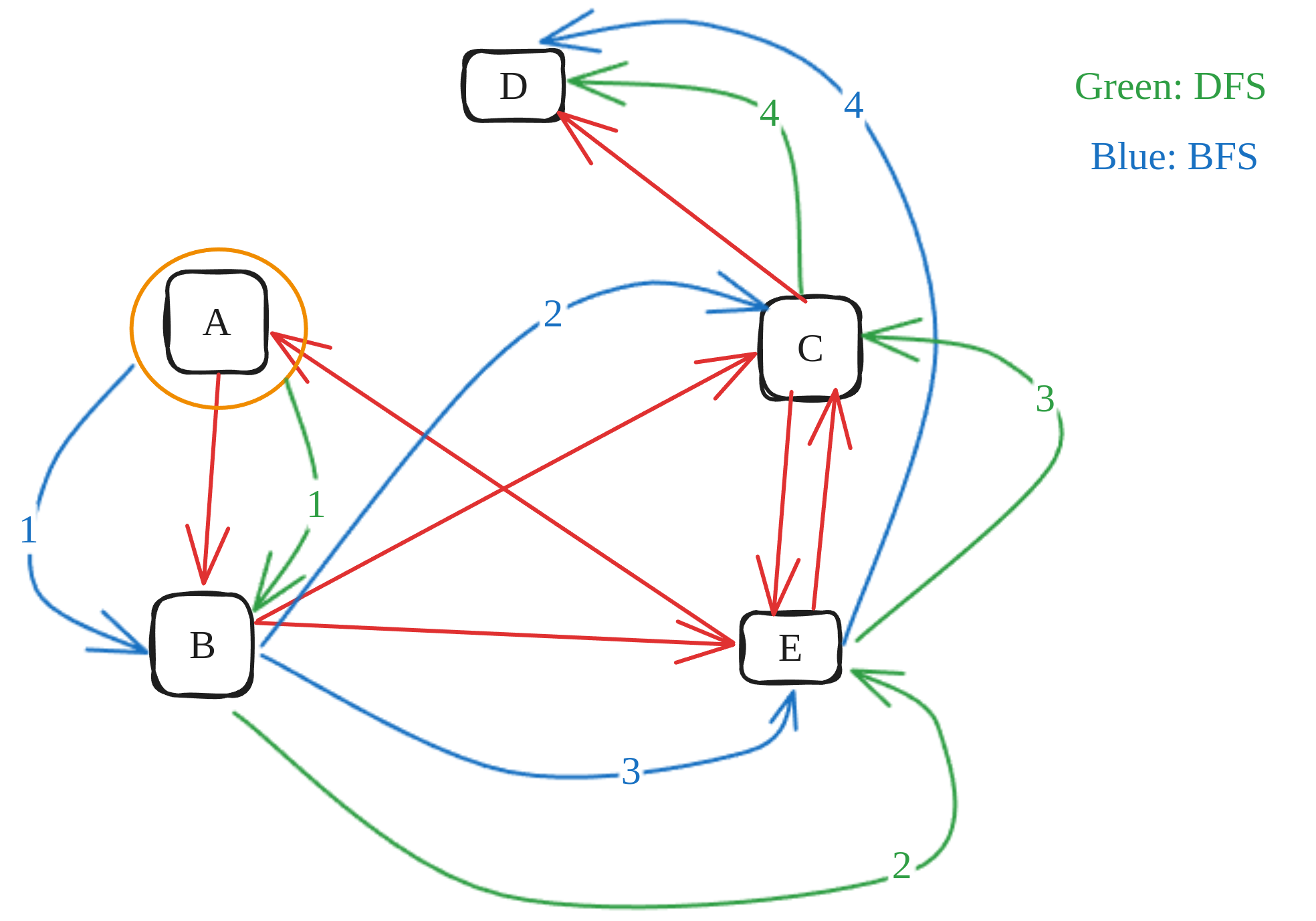
DFS in graph

DFS vs BFS

Algorithms

There are 2 different approaches to implement depth first search in graphs: stack and recursive.

Stack

1. Prepare variables
   • to_visit: A stack to store verteces that needs to be visited. Initial value is the start vertex.
   • visited: A hash set to store verteces that has already been visited. Initial value is the start vertex.
   • path: A list to store all verteces traversed by to_visit.
2. Keep popping to_visit stack while it’s not empty. For each popped vertex:
3. Append the vertex into path
4. Grab the adjacent verteces of the popped vertex. For each adjacent vertex:
5. If the vertex has already been visited, we continue to the next adjacent vertex.
6. Otherwise, we append the vertex into to_visit and visited.

Recursive

Implementation

To see the complete code, go to Code

Stack

    def dfs(self, start: _Vertex) -> list[_Vertex]:
        to_visit: list[_Vertex] = [start]
        visited: set[_Vertex] = {start}
        path: list[_Vertex] = []
 
        while len(to_visit) != 0:
            curr = to_visit.pop()
            path.append(curr)
 
            for neigh in self._get_neighs(curr):
                if neigh not in visited:
                    to_visit.append(neigh)
                    visited.add(neigh)
 
        return path
 
    @abstractmethod
    def _get_neighs(self, vertex: _Vertex) -> list[_Vertex]: ...

Recursive