Binary Tree Traversal Algorithms

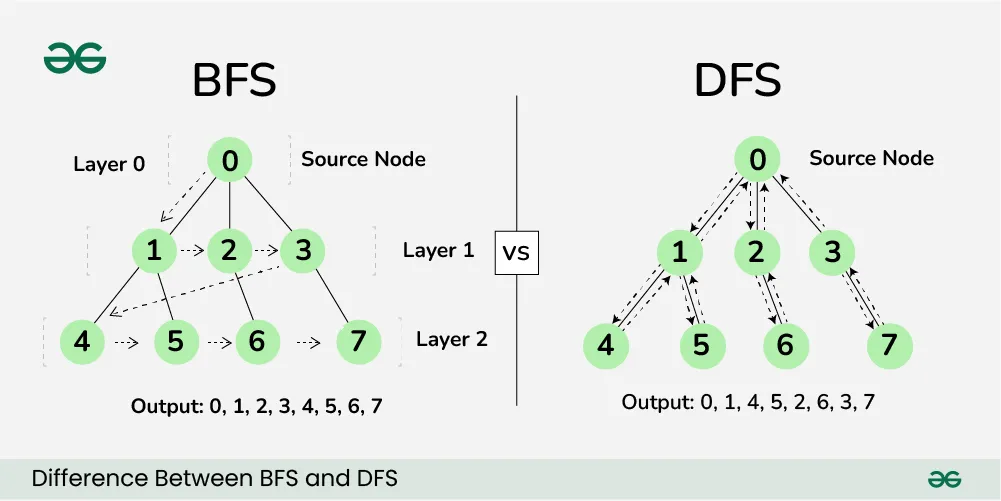
Depth-first search

• Pre-order: Root $\to$ Left $\to$ Right
• In-order: Left $\to$ Root $\to$ Right
• Post-order: Left $\to$ Right $\to$ Root

TIP

Look at the location of the root node.

Breadth-first search

Traverse a binary search tree by level/layer, starting from highest depth to lowest depth.

Algorithm:

1. Create a queue, starting with the root node.
2. While the queue is not empty: 3. Dequeue a node from the queue. 4. Print the node. 5. Add nodes left and right of the dequeued node to the queue.

Implementation

type _Node = Node | None
 
@dataclass
class Node[T]:
    data: T
    left: _Node = None
    right: _Node = None
 
    @staticmethod
    def dfs_inorder(root: _Node) -> None:
        if root is None:
            return
        Node.dfs_inorder(root.left)
        print(root.data)
        Node.dfs_inorder(root.right)
 
    @staticmethod
    def dfs_postorder(root: _Node) -> None:
        if root is None:
            return
        Node.dfs_postorder(root.left)
        Node.dfs_postorder(root.right)
        print(root.data)
 
    @staticmethod
    def dfs_preorder(root: _Node) -> None:
        if root is None:
            return
        print(root.data)
        Node.dfs_preorder(root.left)
        Node.dfs_preorder(root.right)
 
    @staticmethod
    def bfs(root: _Node) -> None:
        if root is None:
            return
        queue: list[Node] = [root]
        while queue:
            node = queue.pop(0)
            print(node.data)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
 
a = Node("a")
b = Node("b")
c = Node("c")
d = Node("d")
e = Node("e")
f = Node("f")
g = Node("g")
 
a.left = b
a.right = c
b.left = d
b.right = e
c.left = f
c.right = g
 
print('=' * 10, "BFS", '=' * 10)
Node.bfs(a)
print('=' * 10, "DFS In-Order", '=' * 10)
Node.dfs_inorder(a)
print('=' * 10, "DFS Pre-Order", '=' * 10)
Node.dfs_preorder(a)
print('=' * 10, "DFS Post-Order", '=' * 10)
Node.dfs_postorder(a)