4.1 Limits of Function

<< 3.6 Properly Divergent Sequences | 4.2 Limit Theorems >>

Summary

Definition

• Cluster point
• Limit of a function

Theorem

Let

• $c\in \mathbb{R}$
• $A\subseteq \mathbb{R}$
• $f:A\to \mathbb{R}$
• $L\in \mathbb{R}$

Then

1. $c$ cluster point of subset of $A$
   • $⟺$ $\exists (a_n)\in A\ni \lim (a_n)\wedge a_n\ne c,\forall n\in \mathbb{N}$
2. $c$ cluster point of $A$
   • $⟹$ $f$ have only 1 limit at $c$
   • ${\lim }_{x\to c}f=L$
     • $⟺$ $\forall V_{\epsilon }(L),\exists V_{\delta }(c)\ni x\in V_{\delta }(c)\cap A,x\ne c⟹f(x)\in V_{\delta }(L)$
     • $⟺$ $\forall (x_n)\in A,(x_n)\to c,x_n\ne c\forall n\in \mathbb{N}⟹(f(x_n))\to L$
   • ${\lim }_{x\to c}f\ne L$
     • $⟺$ $\exists (x_n)\in A,(x_n)\to c,x_n\ne c\forall n\in \mathbb{N}\ni (f(x_n))\nrightarrow L$
   • ${\lim }_{x\to c}f$ does not have a limit at $c$
     • $⟺$ $\exists (x_n)\in A,(x_n)\to c,x_n\ne c\forall n\in \mathbb{N}\ni (f(x_n))$ diverges

---

4.1.1 Definition: Cluster point

Let

• $A\subseteq \mathbb{R}$
• $c\in \mathbb{R}$

If

• $\forall \delta >0,\exists x\in A,x\ne c\ni |x-c|<\delta$

Then

• We say that $c$ is a cluster point of $A$

This definition is rephrased in the language of neighborhoods as follows:

A point $c\in \mathbb{R}$ is a cluster point of $A$ if every $\delta$-neighborhood $V_{\delta }(c)=(c-\delta ,c+\delta )$ of $c$ contains at least one point of $A$ distinct from $c$.

Intuition

$c$ is a cluster point of $A$ if ANY open interval around $c$ contains at least one element of $A$ (that is not $c$ itself).

For example, if $A:=\{1,2\}$, then the point $1$ is not a cluster point of $A$, since choosing $\delta :=\frac{1}{2}$ gives a neighborhood of $1$ that contains no points of $A$ distinct from $1$.

The same is true for the point $2$, so we see that $A$ has no cluster points.

See also:

• https://www.youtube.com/watch?v=McJ7RWs_trY

4.1.4 Definition: Limit of a function

Let

• $A\subseteq \mathbb{R}$
• $c$ be a cluster point of $A$.
• $f:A\to \mathbb{R}$
• $L\in \mathbb{R}$

If

• $\forall \epsilon >0,\exists \delta >0\ni 0<|x-c|<\delta ,\forall x\in A⟹|f(x)-L|<\epsilon$

Then

• We say that $L$ is a limit of $f$ at $c$

Intuition

There are several ways to interpret this definition:

• If we can keep taking any number between $f(x)$ and $L$ infinitely, then $f(x)$ is continuous at $L$.
• If the “distance” between $f(x)$ and $L$ is infinitesmally small, then $f(x)$ is continuous at $L$.

And so on…

Purpose of cluster points

Main purpose of a cluster point is that in this theorem, if $c$ is a cluster point of $A$ and $A$ is the domain of $f$ then ${\lim }_{x\to c}f(x)$ must exist.

In other words, for $f$ to have a limit, $c$ must be a cluster point of the domain of $f$ (which is $A$).

NOTE

1. $\delta (\epsilon )$ is used to conceptually suggest that the value of $\delta$ depends on $\epsilon$
2. $|x-c|>0$, because $x\ne c$ per 4.1.1 Definition: Cluster point
3. We use the following to define limits:

• $f(x)\to L$ as $x\to c$
• ${\lim }_{x\to c}f(x)$
• ${\lim }_{x\to c}f$

4. If ${\lim }_{x\to c}f(x)=L$, then we say $f$ converges to $L$ at $c$
5. If $f$ doesn’t have a limit at $c$, then we say $f$ is divergent at $c$

---

4.1.2 Theorem

Let

• $A\subseteq \mathbb{R}$
• $c\in \mathbb{R}$

If

• $\exists (a_n)\in A\ni \lim (a_n)=c,a_n\ne c,\forall n\in \mathbb{N}$

Then

• $c$ is a cluster point of a subset of $A$

4.1.5 Theorem

If $f:A\to \mathbb{R}$ and if $c\in \mathbb{R}$ is a cluster point of $A$, then $f$ can have only one limit at $c$

TIP

We can prove $f:A\to \mathbb{R}$ has a limit if we can prove $c$ is a cluster point in $A$.

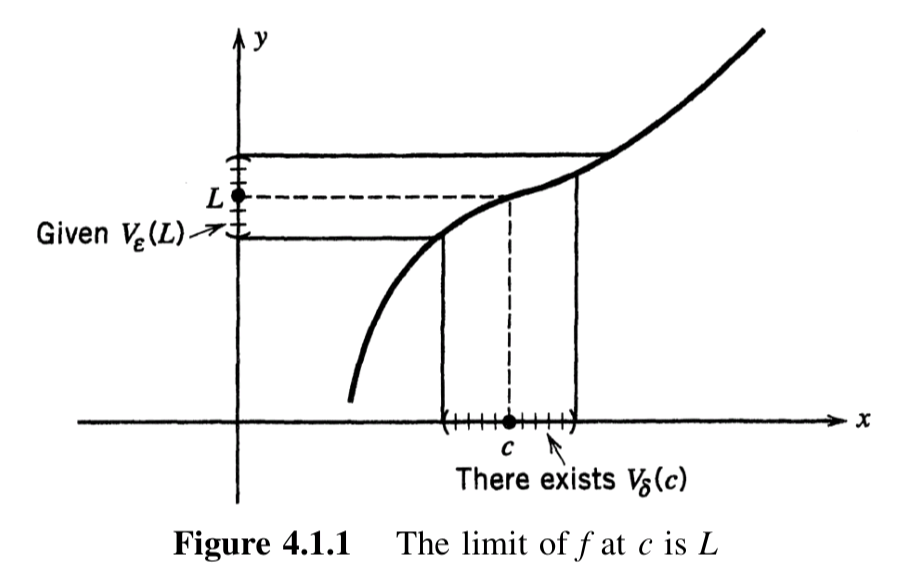
4.1.6 Theorem: Neighborhood definition of limit of function

Let $f:A\to \mathbb{R}$ and let $c$ be a cluster point of $A$.

Then the following statements are equivalent:

1. ${\lim }_{x\to c}f(x)=L$
2. Given any $\epsilon$-neighborhood $V_{\epsilon }(L)$ of $L$, there exists $\delta$-neighborhood $V_{\delta }(c)$ of $c$ such that if $x\ne c$ is any point in $V_{\delta }(c)\cap A$, then $f(x)$ belongs to $V_{\delta }(L)$

NOTE

$x\in V_{\delta }(c)\cap A$ is analogous to $0<|x-c|<\delta ,x\in A$ as in 4.1.4 Definition: Limit of a function

TIP

Limit of function definition in terms of neighborhoods.

If you can visualize limit of function and neighborhood, this should be easy to visualize by intuition.

4.1.8 Theorem: Sequential criterion

Let $f:A\to \mathbb{R}$ and let $c$ be a cluster point of $A$.

Then the following are equivalent:

1. ${\lim }_{x\to c}f=L$
2. For every sequence $(x_n)$ in $A$ that converges to $c$ such that $x_n\ne c$ for all $n\in \mathbb{N}$, the sequence $(f(x_n))$ converges to $L$

TIP

Limit of function definition in terms of converging sequence.

The flow of the definition also resembles function limit definition. If you can visualize converging sequence, this should also be easy to visualize by intuition.

4.1.9 Theorem: Divergence criteria

Let $A\subseteq \mathbb{R}$, let $f:A\to \mathbb{R}$ and let $c\in \mathbb{R}$ be a cluster point of $A$.

1. If $L\in \mathbb{R}$, then $f$ does not have limit $L$ at $c$ if and only if there exists a sequence $(x_n)$ in $A$ with $x_n\ne c\forall n\in \mathbb{N}$, such that the $(x_n)$ converges to $c$ but the $(f(x_n))$ does not converge to $L$

2. The function $f$ does not have a limit at $c$ if and only if there exists a sequence $(x_n)$ in $A$ with $x_n\ne c,\forall n\in \mathbb{N}$, such that $(x_n)$ converges to $c$ but the $(f(x_n))$ diverges

TIP

Number 1 may be used to prove that $f$ does not converge ONLY to $L$ at $c$.

Number 2 may be used to prove that $f$ does not have a limit at all. See 3.4.5: Theorem: Diverging sequence criteria to help.