Number of Solutions of a Linear System

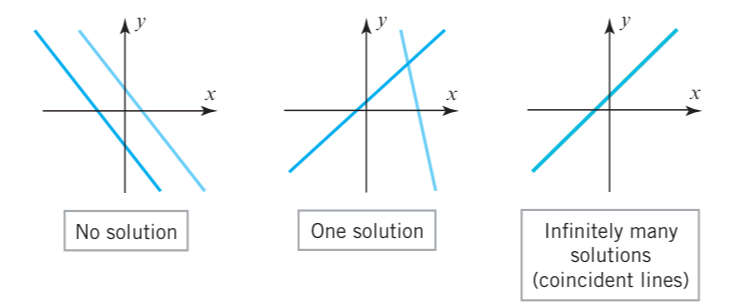
Theorem

Solution of a linear system is either of the following:

1. Zero solution
2. One solution
3. Infinitely many solutions

There are no other possibilities.

Proof

Let $A\mathbf{x}=\mathbf{b}$ be a linear system.

Assume that $A\mathbf{x}=\mathbf{b}$ has more than one solution.

Let ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ be any two distinct solutions (i.e., ${\mathbf{x}}_1\ne {\mathbf{x}}_2$) of $A\mathbf{x}=\mathbf{b}$.

Let ${\mathbf{x}}_0={\mathbf{x}}_1-{\mathbf{x}}_2$.

Because ${\mathbf{x}}_1\ne {\mathbf{x}}_2$, ${\mathbf{x}}_0$ is nonzero (therefore a nontrivial solution); moreover,

$$\begin{array}{rl}A{\mathbf{x}}_0& =A({\mathbf{x}}_1-{\mathbf{x}}_2)\\ & =A{\mathbf{x}}_1-A{\mathbf{x}}_2\\ & =\mathbf{b}-\mathbf{b}\\ & =0\end{array}$$

thus ${\mathbf{x}}_0$ is a nontrivial solution to a homogeneous linear system.

Let $k$ be any scalar. Then,

$$\begin{array}{rl}A({\mathbf{x}}_1+k{\mathbf{x}}_0)& =A{\mathbf{x}}_1+A(k{\mathbf{x}}_0)\\ & =A{\mathbf{x}}_1+k(A{\mathbf{x}}_0)\\ & =\mathbf{b}+k0\\ & =\mathbf{b}+0\\ & =\mathbf{b}\end{array}$$

By definition of solution, we have found that ${\mathbf{x}}_1+k{\mathbf{x}}_0$ is a solution of $A\mathbf{x}=\mathbf{b}$.

Since ${\mathbf{x}}_0$ is nonzero and there are infinitely many choices for $k$, therefore the system of $A\mathbf{x}=\mathbf{b}$ has infinitely many solutions (i.e., we can choose any arbitrary $k$ and $A({\mathbf{x}}_1+k{\mathbf{x}}_0)=\mathbf{b}$ will be true).

Therefore, If $A\mathbf{x}=\mathbf{b}$ has more than one solution, then it has infinitely many solutions.

Lastly, notice that if $A\mathbf{x}=\mathbf{b}$ does not have more than solution, then it either has one solution or zero solution, completing the proof.