Estimating the Model

Fitting a linear model

In the real world, it is often unfeasable to measure every observation in a population. We can approximate a model fit by withdrawing samples from the population instead.

Model fit uses the following notation to differentiate between sample and population model, which is:

$${\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1$$

Coefficient formulas

$$\begin{array}{rl}{\hat{\beta }}_1& =\frac{\sum x_i{y}_i-\frac{1}{n}\sum x_i\sum y_i}{\sum x_i^2-\frac{1}{n}(\sum x_i{)}^2}\\ {\hat{\beta }}_0& =\bar{y}-{\beta }_1\bar{x}\end{array}$$

or, in matrix form,

$$\beta =(X^{T}X{)}^{-1}{X}^{T}y$$

An estimator for error variance

The best estimate of ${\sigma }^2$ is the variance of residual $e_i$, which is the estimate of error ${ϵ}_i$

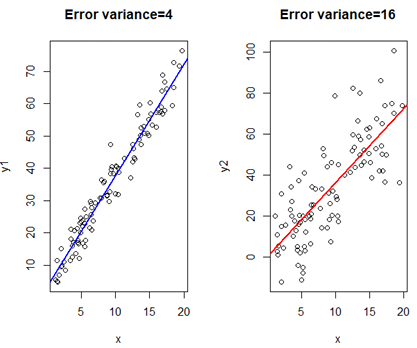
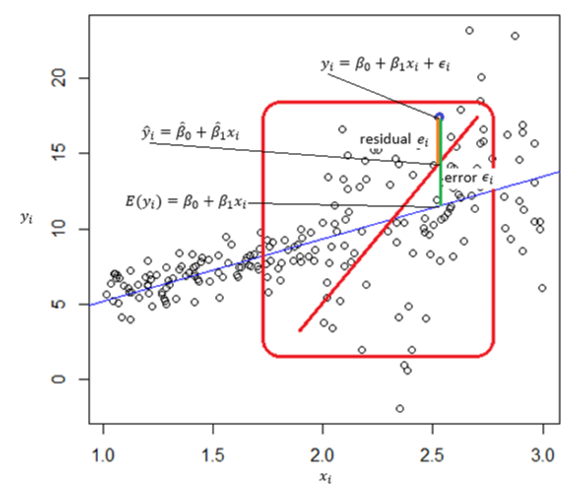
Comparison of regression line using population data and sample data

Regression Equation	Parameters (estimates)	Data	Notes
$E(y_i)={\beta }_0+{\beta }_1{x}_i$	${\beta }_0,{\beta }_1$	Population	Rarely done, since population is not always available
${\hat{y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{x}_i$	${\hat{\beta }}_0,{\hat{\beta }}_1$	Sample	${\hat{\beta }}_0,{\hat{\beta }}_1$ are estimators of ${\beta }_0,{\beta }_1$
${ϵ}_i=y_i-E(y_i)$	Error	Population	Not Known
$e_i=y_i-{\hat{y}}_i$	Residual	Sample	Estimator of ${ϵ}_i$

Formulas

Theoretically,

$$\begin{array}{rl}{\sigma }^2& =\mathrm{Var}(ϵ)\\ & =E[ϵ-E(ϵ){]}^2\\ & =E({ϵ}^2)-E(ϵ{)}^2\\ & =E({ϵ}^2)\\ & ={\int }_{\infty }^{\infty }{ϵ}^{2}f(ϵ)dϵ\end{array}$$

Emprically,

$${\sigma }^2=\frac{{\sum }_{i=1}^N{e}_i^2}{N}=\frac{{\sum }_{i=1}^N(y_i-[{\beta }_0+{\beta }_1{x}_i]{)}^2}{N}=\frac{SSE}{N}$$

Where $N$ is the population size, and SSE is sum of squares error.

$$s^2=\frac{{\sum }_{i=1}^n{e}_i^2}{n-k}=\frac{{\sum }_{i=1}^n(y_i-[{\hat{\beta }}_0+{\hat{\beta }}_1{x}_i]{)}^2}{n-k}=\frac{SSR}{n-k}$$

Where $k$ is the amount of predictor variables, and SSR is sum of squares regression.

Interpretation of $s^2$

We can anticipate that although the predicted value is different from the actual value, 95% of the actual values of $y_i$ are within ${\hat{y}}_i\pm 2s$. A good model should give small $s$.